Plotting a Circle
Plot a circle with radius R, centered at coordinates (x0, y0). We create the circle in polar coordinates and then transform to Cartesian coordinates using the built-in function pol2cart.
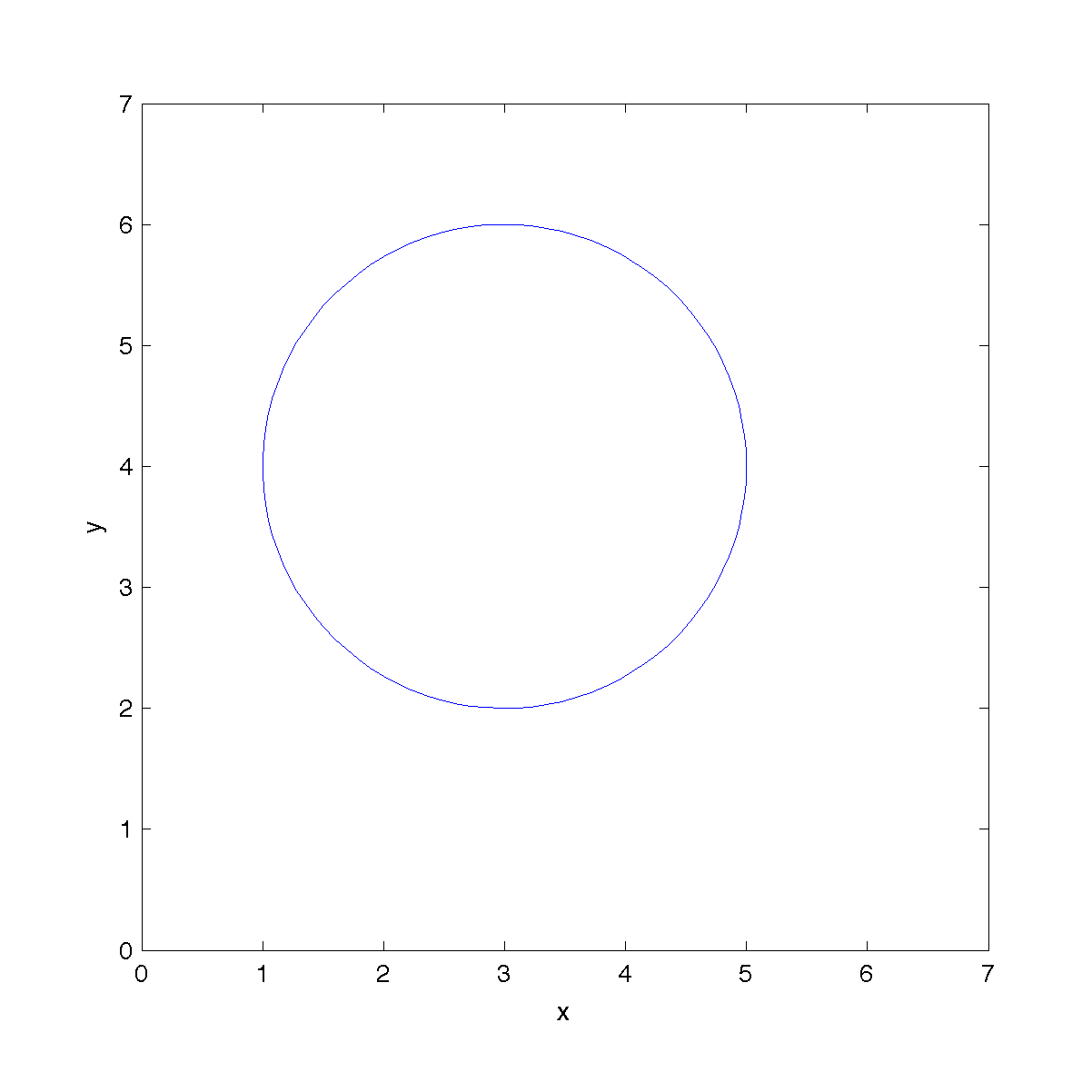
% circlePlot.m % radius = 2; % radius of circle x0 = 3; % x center of circle y0 = 4; % y center of circle N = 100; % number of points used to define circle % create equal length arrays defining a circle in polar coordinates theta = linspace(0,2*pi,N); r = radius * ones(1,N); % convert polar coordinates to Cartesian coordinates [x, y] = pol2cart(theta, r); x = x + x0; % offset the circle so its center lies at (x0, y0) y = y + y0; plot(x,y,'b-'); % plot as blue line xlabel('x') % label axes ylabel('y') axis equal % equal axis scaling so our circle looks circular xlim([0 7]); % set plot limits ylim([0 7]);
Monkey Commentary:
theta = linspace(0,2*pi,N);
This line and the next define a circle in polar coordinates. This line creates an array theta containing N equally spaced numbers ranging from 0 to 2*pi.
r = radius * ones(1,N);
Next, we create an array r that will store the radius for every theta value we defined. The ones(1,N) command creates a 1xN row matrix filled with ones. Multiplying by radius creates an array with the value radius in each element. Given that N = 100 and radius = 2, our arrays will contain the following values:
theta = [0 0.0635 0.1269 0.1904 ...]
r = [2 2 2 2 ...]
[x, y] = pol2cart(theta, r);
The pol2cart function converts polar coordinates (theta, r) to Cartesian coordinates (x,y). This function is equivalent to the following transformation:
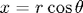
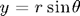
axis equal
The axis equal command ensures that the unit length along the x axis matches the unit length in the y direction, i.e. it guarantees that the circle will look circular.
