Logistic Equation version 1: Super simple code to solve a first-order ODE
In keeping with the monkey tradition, we introduce numerical integration by way of an example. Let's solve the following first-order ordinary differential equation (ODE). This equation is commonly referred to as the Logistic equation, and is often used as an idealized model of how a population (of monkeys for example) evolves as it nears a fixed carrying capacity:
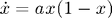
This problem has one free parameter, a, and requires one initial condition,
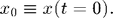
We choose this example because it has a well-known analytic solution, which we can use to check our numerical result:
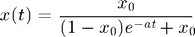
We present three versions of this code. We start simple and add more options and complexity. This first version gives a bare-bones approach.

% logisticV1.m % Numerically integrate a 1D ODE (the Logistic Equation) using the % Runge-Kutta 45 solver function logisticV1 a = 2; % free parameter tBegin = 0; % time begin tEnd = 10; % time end x0 = 0.001; % initial position % Use the Runge-Kutta 45 solver to solve the ODE [t,x] = ode45(@derivatives, [tBegin tEnd], x0); plot(t,x,'ro'); % plot ode45 solution as red circles ylim([0 1.2]); % set y plot limits title('Solution to the Logistic Equation'); % title xlabel('time'); % label x axis ylabel('Monkey Population'); % label y axis %%%%% Function: derivatives % returns the derivative dx/dt for the logistic equation % uses the parameter a from main program, but changeth it not function dxdt = derivatives(t,x) dxdt = a * x * (1 - x); end end
Monkey Commentary
The centerpiece of the code is the ode45 call
[t,x] = ode45(@derivatives, [tBegin tEnd], x0);
This call implements an adaptive-timestep Runge-Kutta integrator. The first argument @derivatives is the name of the function used to calculate the derivatives that define the differential equation. We also pass the time domain to start and stop the integration [tBegin tEnd] and the initial value of x, x0. Because the ode45 solver uses adaptive time steps, the time values in the returned array t will often not be uniformly spaced. The values of the returned array x will correspond to the time values t. To evaluate x at an arbitrary value, see version 3 of this code.
The derivatives function is defined at tha bottom of the code. It simply returns the value of the derivative dx/dt. Notice that the we do not need to pass the parameter a because it is treated as a global variable (MATLAB indicates this by coloring the variable blue-green). MATLAB does have ways of passing parameters to functions, but 4 out of 5 monkeys prefer to just treat the parameters as global variables. This approach simplifies life a bit, it does have two drawbacks: (1) the main code must be defined as a function and (2) we run the risk of overwriting the global varibles unintentionally in some other part of the code.
While the ode45 Runge-Kutta solver works just fine in many cases, MATLAB offers many solvers that are taylored to special circumstances such as stiff equations. So if your code is taking too long to run or crashing you might want to try another solver.
