CRTBP Pseudo-Potential and Lagrange Points

1. Pseudo-Potential

When the motion of the test particle is confined to the plane containing the massive bodies, the acceleration in the rotating reference frame may be written in the form:

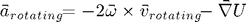
$$ \vec{a}_{rotating} = -2\vec{\omega}\times\vec{v}_{rotating}-\vec{\nabla}U $$
where U is defined as the pseudo-potential. We monkeys define the potential the way physicists do, i.e. in an isolated gravitational well the potential is negative. The celestial dynamics literature often defines U as becoming more positive the deeper one drops into a well. So, if you are a dynamicist, the sign of the potential will look wrong to you.

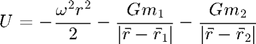
$$ U = -\frac{\omega^2r^2}{2} - \frac{Gm_1}{\left|\vec{r}-\vec{r}_1\right|} - \frac{Gm_2}{\left|\vec{r}-\vec{r}_2\right|} $$
The first term on the right-hand-side generates the centrifugal force. The second and third terms are the gravitational potentials for masses m1 and m2.

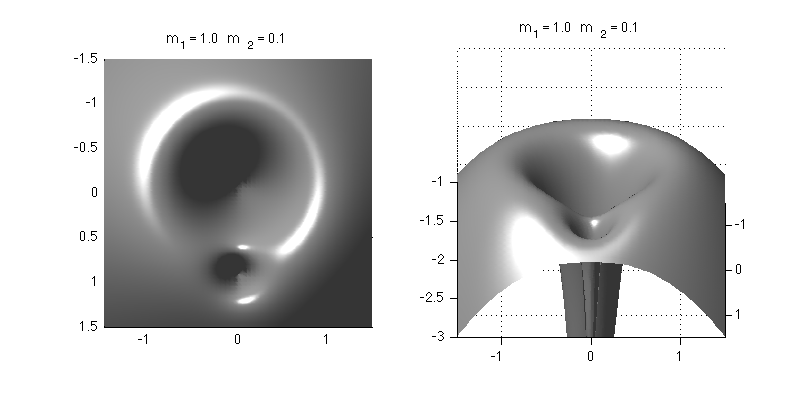
The following figure shows the potential represented as a surface plot for a mass ratio of m2/m1 = 0.1:

Downloads:

Dependent files:

2. Jacobi Integral and Zero-Velocity Curves

While neither energy nor angular momentum are conserved in the rotating reference frame of the CRTBP, there is a quantity that is a constant of the motion. This quantity is called the Jacobi integral:

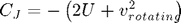
$$ C_J = -\left(2 U + v^2_{rotating}\right) $$
The form of the Jacobi integral is similar to the total energy: it has two terms, one a pseudo-potential and the other a quadratic velocity term like the kinetic energy. The Jacobi integral for a particle will remain constant as it orbits the system. This property may be exploited to place bounds on the particle's motion. For a given Jacobi integral, one can calculate the curve in space where the velocity would go to zero. Such curves are called zero-velocity curves are are equivalent to turning points for potential wells in inertial frames of reference.

The following figure shows zero velocity curves for different Jacobi integrals. The zero-velocity curves bound the shaded 'forbidden' regions where a particle with the specified Jacobi integral can not venture. For example, if a particle with CJ = 4 is initially in orbit around the green planet, it will be stuck there forever (unless it is given a velocity boost by some means). However, the zero-velocity curve for CJ = 3.92 encompasses both m1 and m2. Therefore a particle with this value of CJ can transition back and forth between orbits around each object.

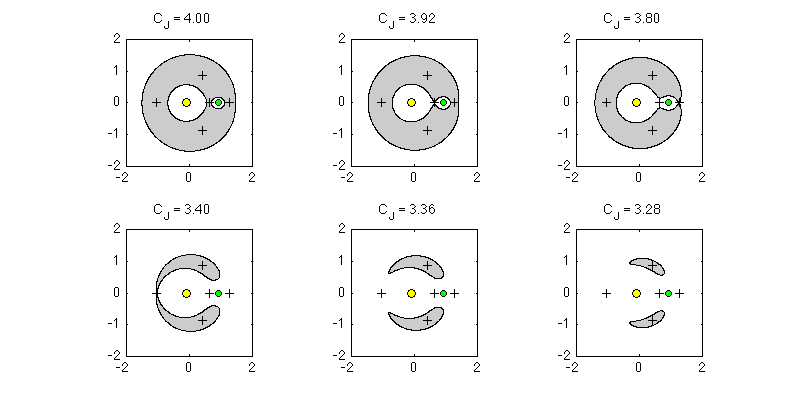
This plot also show the positions of the five Lagrange points (see next section).

Downloads:

Dependent files:

3. Lagrange Points

Lagrange points (a.k.a. libration points) are equilibrium points in the rotating frame. They correspond to places where the pseudo-potential is locally flat. Lagrange showed that there are five such points for any mass ratio m2/m1. Two Lagrange points, L4 and L5, form an equilateral triangle with the two primary masses, one above the masses and the other below. The remaining three Lagrange points L1, L2, L3 lie along the line containing m1 and m2. The positions of the colinear points require solving the roots of a set of fifth order polynomials. The MATLAB program lagrangePoints.m determines the solution numerically for given masses m1 and m2.

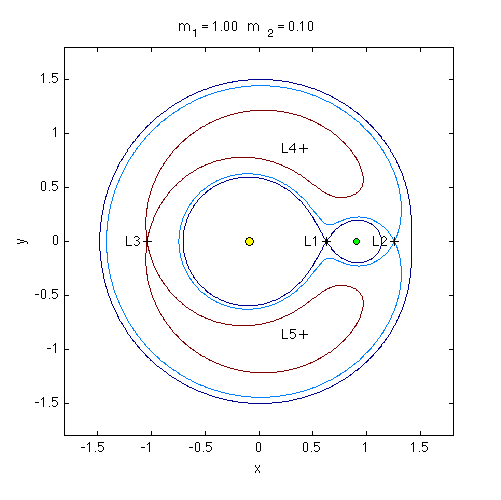
Downloads:

Dependent files:

Home   |   Plot Thumbnails   |   Prev: Plotting   |   Next: Plotting